May 20, 20203 min read

Pythagoras’ Theorem

Updated: Jun 16, 2021

Math Lobby will be going through Pythagoras Theorem today. Pythagoras Theorem is widely used in topics such as trigonometry, real world problems, congruency and similarity and many other topics in the Secondary Math syllabus.

Furthermore, it tested yearly in the O Level E Math, O Level A Math, N Level Math and N Level A Math examination. It will be taught to Secondary 2 and 3 Math students. Without further ado, let us learn how to solve questions using Pythagoras Theorem today!

In this note, you will learn:

1) What is Pythagoras’ Theorem?

2) How to solve questions using the Pythagoras’ Theorem

3) *** BONUS ARTICLE Derivation of the Pythagoras’ Theorem (Visual and Algebraic)

What is Pythagoras’ Theorem?

The Pythagoras’ Theorem is a mathematical fundamental relation derived by the Ancient Greek philosopher, Pythagoras. It basically states that the area of the square with the side of hypotenuse, is the sum of the square of the other two sides in a right-angled triangle which forms the equation: a² + b² = c².

A hypotenuse can be found in two ways:

1) Look for the side that is opposite to the right angle in the triangle

2) The longest side of the triangle. On a first look, this might seem to be quite confusing to understand. Let’s look at the diagram below for a better visualization:

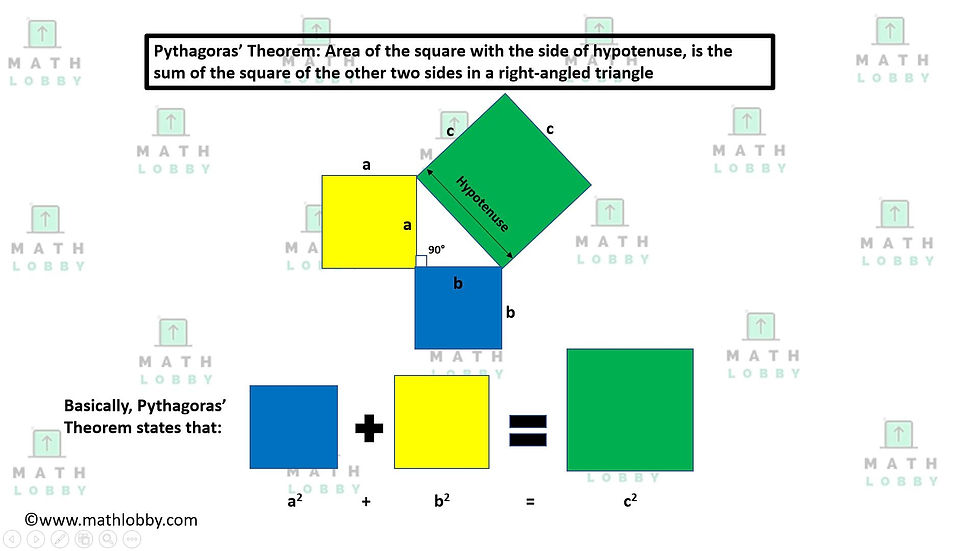
How to solve questions using the Pythagoras’ Theorem

In secondary school mathematics, knowing the true value of Pythagoras’ Theorem can allow us to solve many questions that involve right-angled triangles, including many real-life problems.

Math Lobby Pythagoras Theorem Real World Context Question:

In a construction site, in order to get up to the second level of Building A, workers will have to climb a ladder from the ground floor. However, a new safety measure has been implemented: The base of the ladder must be at least 5m apart from the base of the building. Given that the height from the base of the building to the second level is 6m and the building is perpendicular to the ground, how long must the ladder at least be in order for it to fulfil the new safety measure implemented?

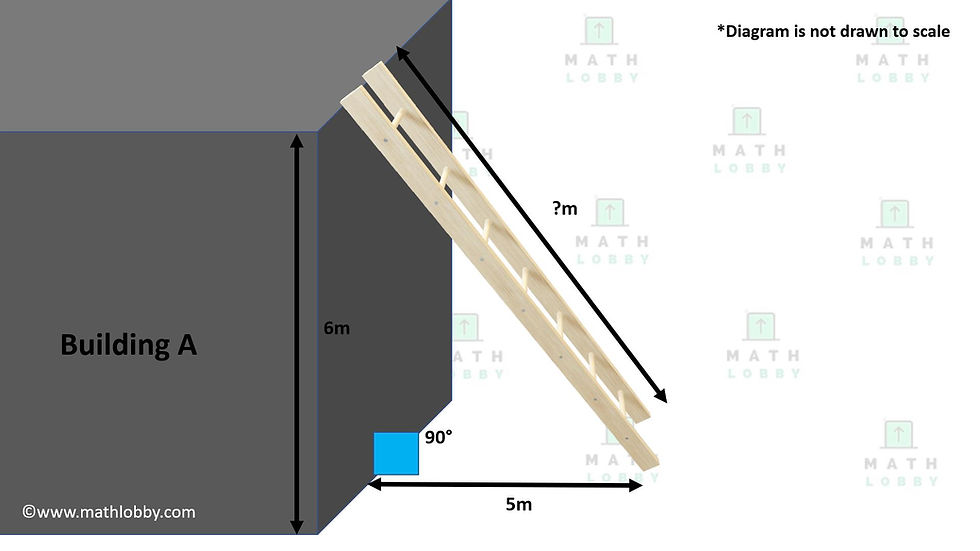
Now, let’s take a look at the diagram. We are provided with the height of the building, which is 6m, and the distance from the base of the building to the base of the ladder to be 5m. The building is perpendicular to the ground; hence it must be a right angle (90°). So, what can we deduce from this?

Yes, it is a right-angled triangle, with the sides of 6m & 5m, and what we are tasked to find is the length of the ladder, which is actually the hypotenuse of the triangle!

Hence, in order to find the length of the ladder, according to Pythagoras’ Theorem: a² + b² = c², we must substitute the values into the formula. Let’s see how we can do this:

Let a be the height of the building, b be the distance between the base of the building and the base of the ladder and c to be the length of the ladder,

By Pythagoras’ Theorem, a² + b² = c²

(6)² + (5)² = c²

36 + 25 = c²

c² = 61

Therefore, c = √ 61

= 7.81024967591m

~ 7.81m(corrected to 3s.f.)

And there you have it! This is how you solve questions using the Pythagoras’ Theorem! Isn’t that easy?

Math Lobby Pythagoras Theorem Questions:

Given a right-angled triangle with the sides a & b, with a hypotenuse c,

Find:

1) c when a = 5cm, b = 7cm

2) a when b = 8cm, c = 20cm

3) b when a = 6cm, c = 18cm

Additional Brain Food!

Now we know how Pythagoras’ Theorem works, but how did it come about? Interested to find out? Click the link below and you can see how it was derived!

Derivation of the Pythagoras’ Theorem (Visual and Algebraic) (Article to be released on 21st May 2020)

That’s all for today, and Math Lobby hopes that you have learnt what Pythagoras’ Theorem is about, and how we can use it to solve theoretical questions in the real world. The Pythagoras’ Theorem can be very useful in our daily life, especially when it comes to architecture and design related fields, which is why learning about Mathematics is so important!

Work hard, stay motivated and we wish all students a successful and enjoyable journey with Math Lobby!

If you want more Secondary Math Tips, FOLLOW our Instagram page at https://www.instagram.com/mathlobbymotivation/

Visit our Website at: www.mathlobby.com

LIKE our Facebook page at www.facebook.com/mathlobbymotivation/

For Secondary Math Tuition, visit: https://www.mathlobby.com/math-tuition

For more Study tips and examination strategies, visit: https://www.mathlobby.com/studytips

For more Study motivation, visit: https://www.mathlobby.com/study-motivation