Basic Algebra and Manipulation
- Math Lobby
- Jul 20, 2020
- 5 min read
Updated: Jun 22, 2021

Dear Secondary Math students, we will be going through Basic algebra and manipulation today. Algebra is tested in all levels of Secondary Math including the O Level E Math, A Math, N Level Math and A Math examinations.
Algebra is connected to many different topics such as Trigonometry, Pythagoras Theorem, Direct and Indirect Proportion, Simultaneous Equations etc. Hence, this is in fact the most important fundamental topic which we urge all students to practice and master.
Without further ado, let's learn more about Algebra today!
What is algebra and the basics of it
· Definition of algebra and its symbols
By mathematical definition, algebra is a part of mathematics which uses letters and symbols to represent numbers and quantities in formulae and equations.
We typically use algebra when we are trying to solve for an unknown value of something, in the form of creating new equations based on different scenarios but still applying specific formulae that doesn’t breach the laws of mathematics.
Let’s take a look at an example of an algebraic expression below:
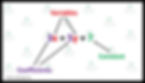
What we have are some numbers and letters from the English alphabet, but what do they stand for?
The numbers that you see in purple, which are accompanied by the red letters, are called coefficients. Coefficients simply represent the number of a particular unknown quantity that you have in an expression.
The letters you see in red, on the other hand, are called variables. Variables are used as a form of substitute for an unknown in a question, and they can vary and take on different values. (Hence the name “variable”)
The number you see in green are called constants. The reason why they are called constants is because they hold the true value as you see it in an expression/equation, and they do not vary in values unlike variables.
Let’s take a look at an example of how we can form an algebraic expression:
I have some apples and oranges in a bag. Timmy then gave me more apples and oranges, which makes the total number of apples I have three times of the initial number of apples, and the total number of oranges I have two times of the initial amount. Jack then took 2 apples and 5 oranges away from me. Form an expression in terms of x and y to represent the scenario at the end.
From here, we can let the number of apples in the bag be x, and the number of oranges in the bad be y. After Timmy gave me more apples and oranges, I have three times the initial number of apples and two times the initial amount of oranges.
This means that I will have 3x + 2y worth of apples and oranges. Then, since Jack took 2 apples and 5 oranges away from me, the final expression would be: 3x – 2 + 2y – 5

· Evaluation of an algebraic expression
Evaluating an algebraic expression basically means substituting different values into the variables in the expression to see what values we yield from it.
For example:
Given an algebraic expression, 10x + 8y + 6, solve for the values of the expression if
a) x = 1, y = 2
b) x = 4, y = 3
Solution:
a) Substitute x = 1, y = 2 into 10x + 8y + 6
10(1) + 8(2) + 6 = 10 + 16 + 6 =32
b) Substitute x = 4, y = 3 into 10x + 8y + 6
10(4) + 8(3) + 6 = 40 + 24 + 6 = 70
· Addition and subtraction of like and unlike terms
In algebra, the addition and subtraction of terms can be tricky. Usually for constants, we can simply add them up to give us a new value, but as for algebra, you can only do that to its coefficient if the terms are like terms, meaning that the terms have the same type of variable i.e. 3x + 5x = 8x, 4y + 8y = 12y
However, for terms that have different type of variables, they are called unlike terms and they cannot be combined with each other, meaning that their simplest form will be separated by a mathematical sign
i.e. 3x + 4y, 6y + 12z
· Simplification of algebraic expressions of terms with different denominators
Simplification of algebraic expressions involving terms with different denominators is actually very simple. All you have to do is to find the lowest common multiple, or LCM, of the denominators to simplify and combine the terms into a fraction.
i.e. Given that we have 1/2x and 1/2y, the lowest common multiple of the denominators is the product of 2x and 2y, which gives us 4xy. In addition and subtraction of fractions, whatever we do to the bottom must be done to the top as well, and vice versa.
Hence, we will have (2y + 2x)/ 4y.
· Distributive Law

Distributive Law states that multiplying a number by a group of numbers added together is the same as doing each multiplication separately.

When you are solving for algebraic expressions containing brackets, always remember to simplify the terms in the brackets first. If there are more than one brackets, then start with the most inner bracket.
You can use PEMDAS as a guide to know in which order the terms must be solved. First will be parenthesis, or brackets, followed by exponents then multiplications and divisions and lastly, additions and subtractions.
· Factorization of algebraic expressions
Factorizing algebraic expressions is actually really easy as well, you just have to bring out the common factors of the terms in the expression, then bracket up the terms remaining just as it is. It is done like so:

And that’s all for today, students! Math Lobby hopes that after this article, you have a clear understanding on the basics of algebra, and is equipped with the necessary skills to deal with questions involving algebraic expressions!
Furthermore, we will be uploading questions on basic algebra and manipulation soon for you to put on your thinking caps so that you can practice and sharpen your algebraic techniques, so stay tuned to find out!
If you have any pending questions, please do go on to our Facebook page, Instagram or contact us directly at Math Lobby! We have certified mathematics tutors to aid you in your journey to becoming a better student!
As always: Work hard, stay motivated and we wish all students a successful and enjoyable journey with MathLobby!
If you want to receive more Secondary Math Tips from us,
Visit and LIKE our Facebook page at www.facebook.com/mathlobbymotivation/
Visit and FOLLOW our Instagram page at https://www.instagram.com/mathlobbymotivation/
Visit our Website at: www.mathlobby.com
Contact us via SMS/WhatsApp/Telegram/Call +65 96322202
*
*
*
#mathlobby #mathlobbymotivation #bestmathtuition #mathtuitionpotongpasir #mathtuitionsg#freemathresources #sgmaths #sgmathtutor #emath #amath #secschool #mathtutorsg #sgedu#nleveltuition #mathtuition #secondarymath #mathtutors #tuitionsg #singaporemath #sgtuition#sgstudents #sgmath #singaporetuition #mathstuition #math #maths #mathtutor #tuition#sgparents #secondaryschool
